Mathematics represents a very high level of abstraction attained by human brain. In ancient India, roots to mathematics can be traced to Vedic literature, which are around 4000 years old. Between 1000 BC and 1000 AD, a number of mathematical treatises were authored in India.
Will Durant, American historian (1885-1981) said that India was the mother of our philosophy of much of our mathematics.
It is now generally accepted that India is the birth place of several mathematical concepts, including zero, the decimal system, algebra and algorithm, square root and cube root. Zero is a numeral as well as a concept. It owes its origin to the Indian philosophy which had a concept of “sunya“, literal translation of which is ‘void‘ and zero emerged as a derivative symbol to represent this philosophical concept.
Geometrical theories were known to ancient Indians and find display in motifs on temple walls, which are in many cases replete with mix of floral and geometric patterns. The method of graduated calculation was documented in a book named “Five Principles” (Panch-Siddhantika) which dates to 5th Century AD. A. L. Basham, an Australian Indologist, writes in his book, The Wonder That was India that “… the world owes most to India in the realm of mathematics, which was developed in the Gupta period to a stage more advanced than that reached by any other nation of antiquity.”
The success of Indian mathematics was mainly due to the fact that Indians had a clear conception of the abstract number as distinct from the numerical quantity of objects or spatial extension.
Algebraic theories, as also other mathematical concepts, which were in circulation in ancient India, were collected and further developed by Aryabhatta, an Indian mathematician, who lived in the 5th century, in the city of Patna, then called Pataliputra. He has referred to Algebra (as Bijaganitam) in his treatise on mathematics named Aryabhattiya.
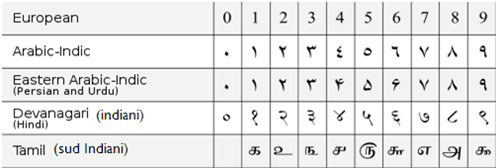
Decimal system origionated in India between 400 B.C. to 400 A.D. The system was adopted by the Arabs by about A.D. 800 at the very earliest. They brought it to Spain about 900. In 1202, Leonardo Fibonacci, an Italian mathematician wrote a hugely influential book called “Liber Abaci” (Book of Calculation), in which he promoted the use of the Hindu-Arabic numeral system. Fibonacci called number “Numeri Indian” (Indian Numbers).
Another mathematician of the 12th century, Bhaskaracharya also authored several treatises on the subject – one of them, named Siddantha Shiromani has a chapter on algebra. He is known to have given a basic idea of the Rolle’s theorum and was the first to conceive of differential calculus.
In 1816, James Taylor translated Bhaskaracharya’s Leelavati into English. Another translation of the same work by English astronomer Henry Thomas Colebruke appeared next year in 1817.
The credit for fine-tuning and internationalizing these mathematical concepts – which had originated in India – goes to the Arabs and Persians. People from Arab and other countries used to travel to India for commerce. While doing commerce side by side, they also learnt easy ways to use calculations methods of India. Through them this knowledge reached Europe. It was from this translation of an Indian text on Mathematics that the Arab mathematicians perfected the decimal system and gave the world its current system of numeration which we call the Arab numerals, which are originally Indian numerals.
Al-Khawarizmi, a Persian mathematician, developed a technique of calculation that became known as “algorism.” This was the seed from which modern arithmetic algorithms have developed. Al-Khwarizmi’s work was translated into Latin under the title Algoritmi de numero Indorum, meaning The System of Indian Numerals. A mathematician in Arabic is called Hindsa which means from India.
The 14th century Indian mathematician Madhava of Sangamagrama, along with other mathematicians of the Kerala school, studied infinite series, convergence, differentiation, and iterative methods for solution of non-linear equations.
Jyestadeva of the Kerala school wrote the first calculus text, the Yuktibhasa, which explores methods and ideas of calculus repeated only in seventeenth century Europe.
The Hindu cosmological time cycles explained in the Surya Siddhanta, give the average length of the sidereal year (the length of the Earth’s revolution around the Sun) as 365.2563627 days, which is only 1.4 seconds longer than the modern value of 365.2563627 days. This remains the most accurate estimate for the length of the sidereal year anywhere in the world for over a thousand years.